ALGORITMO DE AJUSTE POLIGONAL: PARALELISMO En el modelo hexagonal se dedicaron unos comentarios a este factor, que era propuesto en [16] para reducir el coste de operaciones del proceso. Se decía entonces que el paralelismo tiene una gran importancia a la hora de una implementación hardware, pero que para el caso de estudio no resulta especialmente provechoso. A pesar de lo anterior, dada la relativa simplicidad de la implementación, se decidió desarrollar el algoritmo haciendo uso del paralelismo: esto supone una forma de recorrer los nodos de la malla, refinándolos, y sin dar prioridad a zonas concretas de la imagen, sino tratando de mejorarla globalmente desde el principio. Para el caso de mallas adaptativas, se ha desarrollado el algoritmo de forma que también hace uso del paralelismo desde el punto de vista teórico, aunque en la práctica se ejecuta secuencialmente. La idea es la misma: durante el proceso de un polígono, los nodos que rodean al que está siendo procesado permanecen fijos; las operaciones quedan restringidas a su interior, y por tanto es posible procesar ese polígono de forma simultánea a otros, siempre que sean totalmente disjuntos (que no compartan triángulos). El principal problema proviene de la estructura irregular de la malla. En el caso regular, los hexágonos eran clasificados en tres categorías, de forma que los de una misma categoría no compartían triángulos y podían ser procesados en paralelo. En este caso no hay nada determinado, por lo que se ha desarrollado un algoritmo que dinámicamente establece las categorías o tipos de polígonos que son necesarias. El proceso es el siguiente: Se toma un primer polígono y se empiezan a recorrer los demás, comprobando que no tengan triángulos en común con el primero. En cuanto alguno lo cumple, se incorpora a la misma categoría que el polígono inicial; pueden seguir recorriéndose los polígonos, pero ahora deben ser disjuntos con los dos polígonos, y así sucesivamente. Tras recorrerlos todos, se tiene un grupo de polígonos de un mismo tipo; se comienza entonces un nuevo recorrido, pero sin tomar ya en cuenta a los polígonos que han sido clasificados. Al terminar con todos los polígonos, se tendrá un cierto número de tipos, cada uno con un número de polígonos. Según la idea del paralelismo, los polígonos de un mismo tipo podrán ser procesados a la vez. 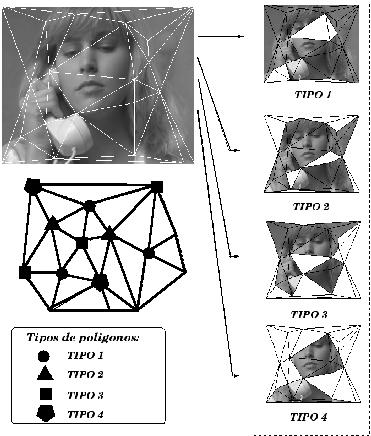En la figura se muestra un ejemplo, en el que se han detectado cuatro grupos de polígonos. Ejemplo del modelo adaptativo. Una vez que se han clasificado los polígonos, el algoritmo comienza el proceso de refinamiento de los vectores con el tipo de polígonos que cubra un mayor porcentaje del área de la imagen. De esa forma, al terminar de refinar los nodos en los que están centrados esos polígonos se habrá producido una mejora global en la escena (como sucedía con el caso regular). En la imagen puede verse que los polígonos del tipo 1 cubren una mayor área que los del tipo 2, y así sucesivamente. En cuanto a los huecos que aparecen en las imágenes podrían evitarse mediante la adecuada modificación del método de triangulación. Hay que señalar que el algoritmo desarrollado no es óptimo, porque puede llegar a distintos resultados según el orden en el que se realice el recorrido de los polígonos, y esto también depende del método de triangulación. Como posible solución pueden introducirse restricciones en el algoritmo, de forma que se llegue a soluciones particulares de interés: en un caso hardware dependería de los recursos de los que se disponga, pero en cualquier caso interesa equilibrar la carga de los procesadores de los que se disponga.