Image Processing Group (GTI), Universidad Politécnica de Madrid
3D Reconstruction with the Minimum Number of
Square-pixel Uncalibrated Cameras
Given a set of images of a static scene, we address the problem of recovering the camera parameters solely from image measurements (without any knowledge about the scene). In computer vision, this problem is known as the autocalibration or self-calibration of the cameras. More specifically, this problem arises if there is a projective reconstruction of the scene (i.e., a reconstruction that differs from the true acquired scene by a projective transformation) and we wish to obtain a Euclidean reconstruction (i.e., one that differs from the true scene in a similarity transformation, which consists of a rigid body motion and a scaling). Geometrically, it is well known that the solution of the problem is equivalent to the estimation of the absolute conic, which lies in the plane at infinity.
To solve the autocalibration problem, some data about the camera must be available. We address the problem of autocalibration in its less restrictive setting in practice: cameras with arbitrarily varying parameters with the exception of the pixel shape, which is assumed to be known. It can be easily seen that this is equivalent to having cameras with square pixels. In the past, algorithms based on this restriction have been proposed that result in a set of linear equations, but with the drawback of requiring 10 or more cameras. These algorithms are inspired by the geometric observation that, from the optical center of each square-pixel camera, two lines can be identified in the projective reconstruction that must intersect the absolute conic. The absolute quadratic complex (AQC) encodes the set of lines intersecting this conic.
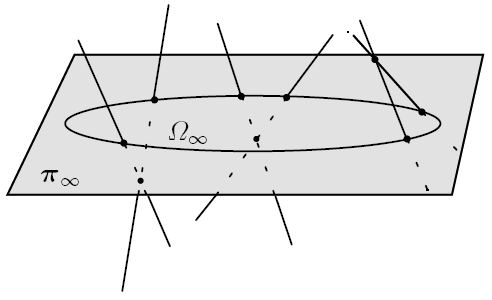
Illustration of the incidence relations between the isotropic lines
of three cameras, the plane at infinity and the absolute conic.
However, an informal parameter count reveals that far fewer cameras are theoretically sufficient. The autocalibration problem has 8 unknowns, which correspond to the degrees of freedom (dof) needed to determine the plane at infinity (3 dof) and the absolute conic within it (5 dof). Knowing camera skew and aspect ratio amounts to two equations per camera and thus at least 4 cameras should be given in order to solve the problem. Given the non-linear nature of these equations, multiple solutions can be expected and so 5 cameras should be the minimum required to obtain, generically, a unique solution.
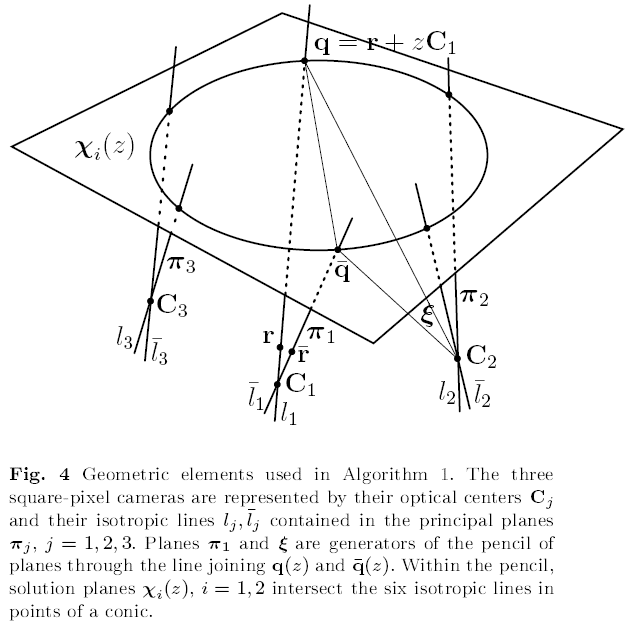
The main aim of this work is to obtain a Euclidean reconstruction from the minimum number of cameras using exclusively the pixel shape restriction. The geometric object that will be employed for this purpose is the variety of conics intersecting six given spatial lines simultaneously, which will be termed the six-lines conic variety (SLCV). In this paper we are interested in the SLCV given by the absolute conic at infinity.
The SLCV for six lines in generic position can be identified with a surface of P3* (i.e., the projective space given by the planes of space) of degree 8. We prove that this degree reduces to 5 in the case of the three pairs of isotropic lines of three square-pixel cameras. We show that the fifth-degree SLCV has three singularities of multiplicity three, given by the three principal planes of the cameras. This result is used in to generate a bidimensional parameterization of the candidate planes at infinity compatible with three square-pixel cameras. This parameterization, together with the additional data given by another two or more square-pixel cameras permits to identify the true plane at infinity through a two-dimensional optimization process. However, the technique could as well use other additional data such as some scene constraints (e.g. vanishing points detected in the images).
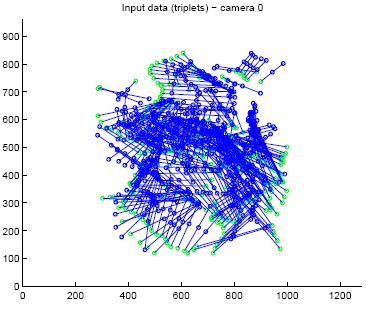
Sample acquired images from the view point of one of the cameras.
Triplets of aligned LEDs in a rigid bar. The triplet structure is used for comparison purposes.
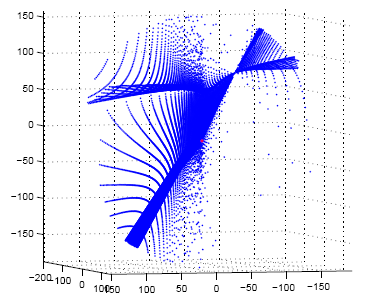
Sampled points of the Six-Line Conic Variety (SLCV).
The dots represent planes in dual space P3*.
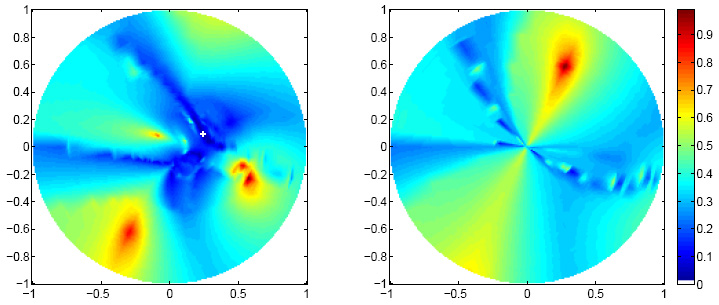
Plots of the sampled cost function.
Left: values at the unit disc of the complex plane, |z|≤1. Right:
values at the complement of the unit dist, at positions 1/conj(z).
The white cross in the left plot marks the location of the minimum.
Sample input images (4 out of 10):


Equivalent focal length is 50 mm.


Equivalent focal length is 100 mm.

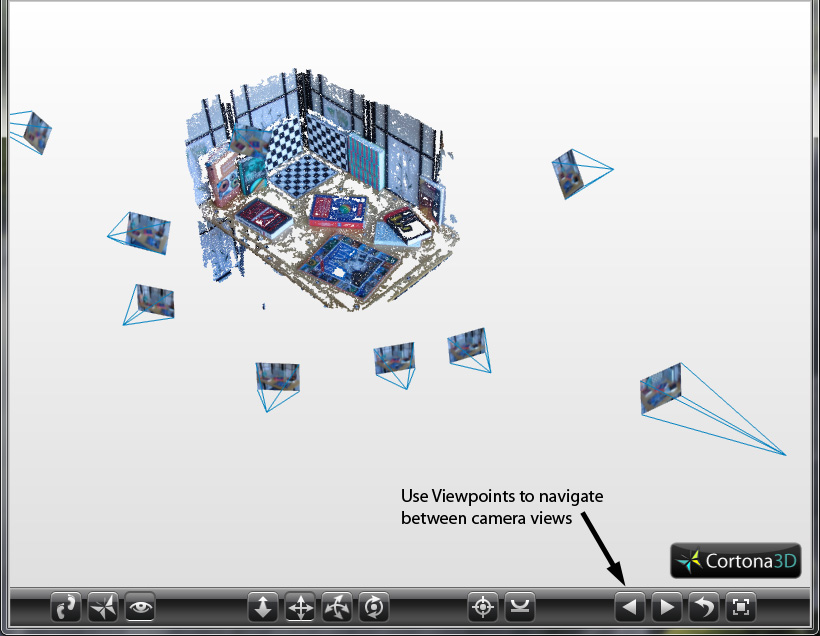
Experiment with 10 images of the Checkerboard dataset: reconstructed 3D scene.
Here is a VRML version of the previous reconstruction.
Downloadable RAR file with VRML scene and images.
Ply file (to visualize with Meshlab)
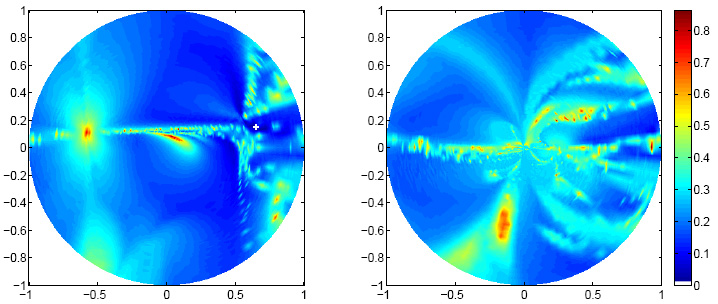
Plots of the sampled cost function.
Left: values at the unit disc of the complex plane, |z|≤1. Right:
values at the complement of the unit dist, at positions 1/conj(z).
The white cross in the left plot marks the location of the minimum.

Experiment with 5 images of the Checkerboard dataset: reconstructed 3D scene.
Here is a VRML version of it.
Downloadable RAR file with VRML scene and images.
Ply file (to visualize with Meshlab)
Also, experiments with real images from an outdoor scene were also conducted. Some images of the Plaza de la Villa in Madrid, with a resolution of 1280 x 960 pixels, were acquired with an OLYMPUS E-620 camera varying the focal length between 50 and 70 mm (in an equivalent 35 mm film).
Sample input images (4 out of 16):


Equivalent focal length is 50 mm.


Equivalent focal length is 70 mm.

Experiment with 16 images of the Plaza de la Villa dataset: reconstructed 3D scene.
Here is a VRML version of it.
Downloadable RAR file with VRML scene and images.
Ply file (to visualize with Meshlab)

Experiment with 5 images of the Plaza de la Villa dataset: reconstructed 3D scene.
Here is a VRML version of it.
Downloadable RAR file with VRML scene and images.
Ply file (to visualize with Meshlab)

| José I. Ronda | e-mail: jir at gti.ssr.upm.es |
| Antonio Valdés | e-mail: Antonio_Valdes at mat.ucm.es |
| Guillermo Gallego | e-mail: ggb at gti.ssr.upm.es |


