Image Processing Group (GTI), Universidad Politécnica de Madrid
3D reconstruction
with uncalibrated cameras.
Camera autocalibration and other
geometry problems in computer vision

What is camera
autocalibration?
Suppose you want to obtain the 3D structure of a scene (3D
positions of points, relative camera positions) from a set
of images and you have no idea about where the cameras
were located or what their internal parameters (focal
length, etc.) were.
Then you can proceed in the following way:
- Mark significant points and their correspondances across the images.
- Obtain from these data a projective reconstruction of the scene, i.e., a distorted 3D reconstruction that is related to the true one by a spacial homography. There are several well-established algorithms for that.
- Find the rectifying homography, i.e., the geometric transformation that will restore the 3D structure from the distorted version. This is the camera autocalibration part, because you get at the same time the camera positions and their internal parameters.
Camera autocalibration is an active are of research because many of the available algorithms are very noise-sensitive, or produce multiple solutions, and also because there are many particular cases that deserve special attention.
This page includes some tutorial information on the topic and introduces the contributions of our group in this field and other geometry problems in computer vision.
Slides of a talk (PDF, in spanish)
Transparencias de una charla (PDF, en español)
Slides of a talk (PDF, in spanish)
Transparencias de una charla (PDF, en español)
|
We address the problem of the Euclidean upgrading of a projective calibration of a minimal set of cameras with known pixel shape and otherwise arbitrarily varying intrinsic and extrinsic parameters. To this purpose, we introduce as our basic geometric tool the six-line conic variety (SLCV), consisting in the set of planes intersecting six given lines in 3D space in points of a conic. We show that the set of solutions of the Euclidean upgrading problem for three cameras with known pixel shape can be parameterized by means of a one-to-two easily computable mapping and, as a consequence, we propose an algorithm that permits to reduce the number of required cameras to the theoretical minimum of 5 cameras to perform Euclidean upgrading with the pixel shape as the only constraint. J. I. Ronda, A. Valdés, G. Gallego, 3D Reconstruction with the Minimum Number of Square-pixel Uncalibrated Cameras. In submission. Pablo Carballeira, José Ignacio Ronda, Antonio Valdés, 3D reconstruction with uncalibrated cameras using the six-line conic variety. In Proceedings of IEEE ICIP 2008: 205-208. DOI: 10.1109/ICIP.2008.4711727 |
 |
|
We address the problem of the recovery of Euclidean structure of a projectively distorted n-dimensional space from the knowledge of the, possibly diverse, lengths of a set of segments. This problem is relevant, in particular, for Euclidean reconstruction with uncalibrated cameras, extending previously known results in the affine setting. The key concept is the Quadric of Segments (QoS), defined in a higher-dimensional space by the set of segments of a fixed length, from which Euclidean structure can be obtained in closed form. We have intended to make a thorough study of the properties of the QoS, including the determination of the minimum number of segments of arbitrary length that determine it and its relationship with the standard geometric objects associated to the Euclidean structure of space. Explicit formulas are given to obtain the dual absolute quadric and the absolute quadratic complex from the QoS. J. I. Ronda, A. Valdés, Euclidean upgrading from segment lengths, International Journal of Computer Vision, vol. 90, no. 3, pp. 350-368, Dec. 2010. DOI: 10.1007/s11263-010-0369-z |
 |
|
This work provides and evaluates
new algorithms for camera autocalibration based on
the set of lines intersecting the absolute conic.
Besides, in order to make the topic more
attractive for the engineering field, a totally
new formulation in terms of Plücker matrices and
Plücker coordinates is developed. For the sake of
completeness, a thorough introduction to Plücker
matrices and coordinates is provided. G. Gallego, J. I. Ronda, A.
Valdés, N. García, Recursive Camera
Autocalibration with the Kalman Filter. In
proceedings of IEEE ICIP (5) 2007: 209-212. DOI: 10.1109/ICIP.2007.4379802. |
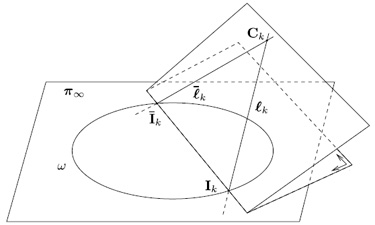
Intersection with the absolute conic ω of the isotropic lines of the k-th camera, with center Ck. |
|
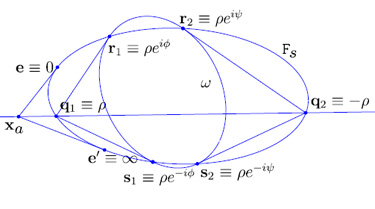
With calibrated cameras you just
need two images to get a Euclidean reconstruction.
However, with uncalibrated cameras you need three
images taken with the same parameters. In this
work we show that if the cameras have square
pixels, with two cameras you almost have
a Euclidean reconstruction, as you can get, in
explicit closed-form, a set of
reconstructions depending on one parameter.
Therefore, if you have a single piece of data from
the scene, such as knowing that two lines are
parallel or orthogonal, it is straightforward to
search the set of solutions for the best-fit case. |
Condition of compatibility of ω with epipolar geometry. |
|
Equivalent to the calibration
pencil is the absolute line quadric
(ALQ), another geometric object that represents
the lines intersecting the absolute conic and can
be directly obtained from the absolute quadric. In
fact, in this (quite mathematical) paper we show
that the ALQ is just the exterior product of the
absolute line quadric with itself and employ this
fact to recover the absolute quadric from the ALQ. José Ignacio Ronda, Guillermo Gallego, Antonio Valdés, Camera autocalibration using Plucker coordinates. In proceedings of IEEE ICIP (3) 2005: 800-803. DOI: 10.1109/ICIP.2005.1530513 |
 |
|
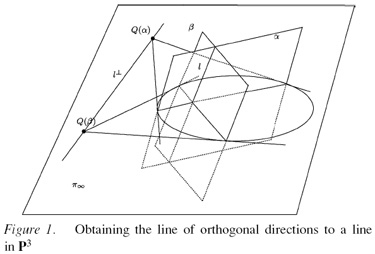
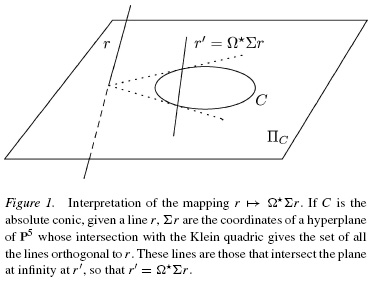
If you have images taken with cameras with square pixels, as most of them are, you have a lot of information in the projective reconstruction that can help you to locate the absolute conic. In fact, for each camera you have two lines that intersect this conic, so that, "all you have to do" is to find a conic that intersects all these lines. A remarkable fact is that, if
you use Plücker coordinates to represent lines,
the set of lines that intersect the absolute conic
is given by a pencil of quadrics (the "calibration
pencil"). This makes autocalibration a problem of
linear algebra: given ten or more cameras, an
homogeneous linear equation gives you the
calibration pencil, and another one extracts the
plane at infinity from the calibration pencil. Antonio Valdés, José Ignacio
Ronda, Guillermo Gallego, Linear camera
autocalibration with varying parameters. In
proceedings of IEEE ICIP 2004: 3395-3398. DOI: 10.1109/ICIP.2004.1421843. |
 |
|
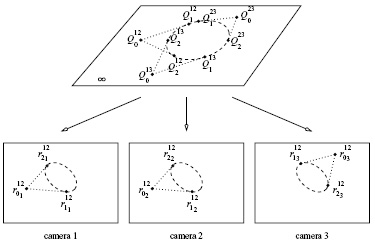
In this work we provide "yet
another algorithm" for the autocalibration of
three or more cameras with arbitrary constant
intrinsic constant parameters. It has a nice
geometrical motivation, based on the horopter
curves associated to each pair of images and the
special way in which they cut the plane at
infinity.
J. I. Ronda, A. Valdés, F. Jaureguizar, Camera autocalibration and horopter curves, International Journal of Computer Vision, vol. 57, no. 3, pp. 219-232, May 2004. DOI: 10.1023/B:VISI.0000013095.05991.55 Paper preprint |
 |
We show that projectively invariant evolution operators have unavoidable singularities. In particular, we see that there exists no non-singular projective evolution operator well-defined over straight lines nor conics.
M. Castrillón and A. Valdés, Projective Evolution of Plane Curves. International Journal of Computer Vision, 42 (3). pp. 191-201, 2001. DOI: 10.1023/A:1011143732632
Paper preprint
Please address your questions or comments to José I. Ronda (jir@gti.ssr.upm.es)
(DBLP bibliography)
or Antonio Valdés
(Antonio.Valdes@mat.ucm.es)
(DBLP bibliography)
Last update: Sept. 29th, 2011.