AJUSTE HEXAGONAL: CONDICIONES DE PROCESO DE UN NODO Al margen del orden seguido para recorrer los nodos, el algoritmo debe establecer unas condiciones que permitan tomar la decisión de procesar o no un nodo (cuando se habla de procesar un nodo o de procesar el hexágono centrado en ese nodo, se entiende que consiste en aplicarle el conjunto de pasos descritos anteriormente). Las condiciones expuestas en [16] son las siguientes: Si un nodo no ha sido procesado anteriormente, debe ser procesado. Si un nodo ha sido procesado anteriormente, debe comprobarse si mejoró, es decir, si la posición que actualmente ocupa no era la que tenía antes de someterlo al último proceso. Si el indicador correspondiente muestra que el nodo mejoró, debe volver a ser procesado. Si un nodo fue procesado pero no mejoró, deben comprobarse los seis nodos adyacentes. En caso de que al menos uno de ellos fuese procesado con posterioridad al nodo que se está considerando y mejorase, debe volver a procesarse el nodo. Es importante subrayar el hecho de que la mejora de alguno de los nodos periféricos fuese posterior. Únicamente en ese caso se habrán vuelto a deformar al menos dos de los triángulos del hexágono (los dos triángulos que tienen en común el nodo central, y el nodo periférico que ha mejorado), por lo que la situación habrá cambiado y el punto central es susceptible de volver a mejorar en el proceso. Si el nodo no cumple ninguna de las condiciones anteriores, no debe volver a procesarse, y hay que pasar a considerar el siguiente nodo. 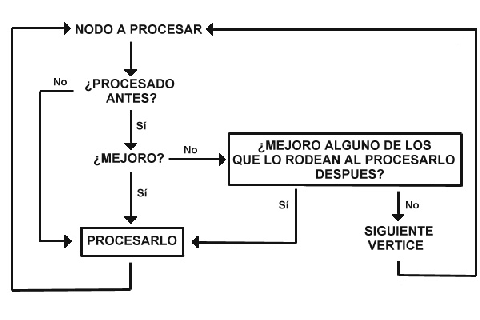En la figura puede verse un esquema del flujo de control que se sigue para la elección de los nodos a procesar. Condiciones para el proceso de los nodos durante el ajuste hexagonal. El algoritmo de ajuste hexagonal hace un recorrido por todos los nodos interiores de la malla, procesando aquellos que cumplen las condiciones anteriores. A medida que se avanza, van siendo menos los nodos que mejoran, por lo que cada vez es necesario procesar un menor número de ellos. Este recorrido puede continuar hasta que ningún nodo mejore, o hasta que se converja hacia mínimos locales o hacia un mínimo global, es decir: puede establecerse un valor fijo para cada nodo particular, de forma que si al procesar ese nodo la diferencia entre la reconstrucción y la imagen original (dentro del hexágono correspondiente) no se disminuye al menos en ese valor, el nodo no vuelve a procesarse. O también puede fijarse un valor para la imagen global, de forma que si tras un recorrido de todos los nodos no se ha conseguido la mejora pretendida, el proceso finaliza. Estas cuestiones se abordarán en el apartado final de resultados.