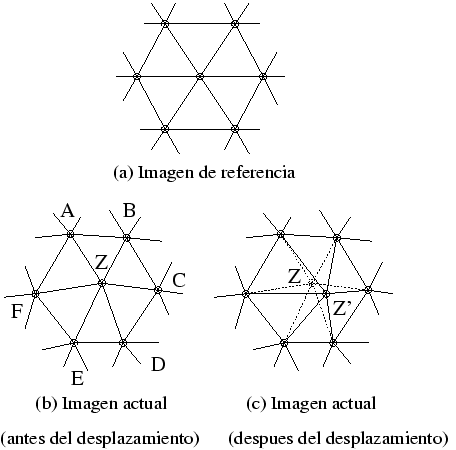
AJUSTE HEXAGONAL: PROCESO DE UN NODO Los pasos del proceso son los siguientes: Se toma un nodo de la malla sobre la imagen actual, al que se llamará Z. Los seis nodos que lo rodean, A-F (ver figura 1 (b)), se mantienen fijos durante los siguientes pasos del proceso, que además consisten en operaciones que quedan restringidas al interior del hexágono que forman esos seis nodos. Después se debe desplazar el nodo elegido a una nueva posición, de forma que pueda comprobarse si así se consigue reducir el error entre la imagen real y la reconstrucción para el interior de ese hexágono. Para desplazar el nodo Z a una nueva ubicación Z' (ver figura 1 (c)) se modifican las componentes del vector de movimiento que apunta a dicho nodo. Figura 1: Ajuste Hexagonal Además, es necesario definir la estrategia de desplazamiento de los nodos, es decir, cuáles van a ser las posibles posiciones a las que se va a desplazar el nodo. 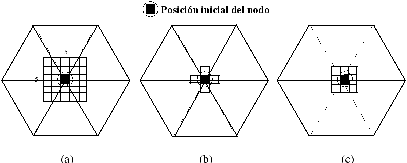Se han considerado e implementado tres posibles mecanismos: En [3] proponen desplazar el nodo por todas las posiciones de una ventana de búsqueda centrada en él, siendo el tamaño de la ventana de MxM píxeles (ver ejemplo de la figura (a) con M=5). Otra alternativa consiste en realizar el desplazamiento de un nodo a las posiciones inmediatamente adyacentes. En este punto se consideran dos posibles soluciones: La primera consiste en desplazar el nodo a las 4 posiciones adyacentes formadas por los puntos superior, inferior, derecho e izquierdo. Esta estrategia de `vecindad 4', que puede verse en la figura (b), es análoga al mecanismo de búsqueda cruzada que se emplea para la estimación de los vectores en algunos modelos, y que fue descrito en el capítulo 2. La otra estrategia consiste en desplazar el nodo a las ocho posiciones adyacentes, que incluyen a las cuatro anteriores más las esquinas, como puede verse en la figura (c). En realidad equivale a una particularización del método de ventana, con M=3, y se puede denominar de `vecindad 8'. Figura 2: Estrategias de Desplazamiento Más adelante se comentarán algunas particularidades de los métodos anteriores, en cuanto a la relación entre calidad que consiguen y tiempo de proceso. Pero conviene aclarar una cuestión: el recorrido que se haga de esas posiciones es independiente del orden. La razón es que no se va a tomar la decisión de desplazar el nodo hasta que se hayan recorrido todas las posiciones, por lo que no importa el orden, sino los resultados de error que se obtienen para cada posición. Una vez que se ha realizado el desplazamiento de un nodo, es evidente que la estructura de los seis triángulos que comparten dicho nodo se habrá visto alterada, y debe actualizarse. De igual forma, los parámetros de la transformación afín asociados a cada triángulo deben volver a calcularse, para aplicar de forma correcta el mecanismo de interpolación que permite obtener los valores de intensidad de todos los píxeles interiores al hexágono. Se lleva a cabo la síntesis de la predicción, pero limitada al interior del hexágono tratado, mediante el mecanismo descrito en el apartado de compensación. Una vez que se ha sintetizado la predicción en el interior del hexágono, se procede a calcular la diferencia entre el cuadro actual y la predicción, también para el interior del hexágono tratado. Esa diferencia se evalúa empleando como medida el error cuadrático medio (ecm). El error calculado se almacena, y se procede a desplazar el nodo central a las restantes posiciones, de acuerdo al criterio seleccionado (4 adyacentes, 8 adyacentes o ventana). Para cada una de esas posiciones se repiten todos y cada uno de los pasos anteriores. Una vez que se han recorrido todas las posiciones, se registra como nueva posición de Z, aquella que minimiza el error calculado y se establecen dos indicadores: uno que informa de que el nodo ha sido procesado, y otro que informa de si en este nodo se ha producido o no mejora. El conjunto de pasos anteriores se aplicarian de igual forma a todos los nodos interiores de la malla, por lo que cada vez que se procesa uno de ellos, se consigue que la diferencia entre la imagen actual reconstruida y la original disminuya, o permanezca constante. Una vez explicado en qué consiste el refinamiento o proceso de un vector, hay que tomar la decisión de establecer las condiciones que indican si un nodo debe ser procesado o no.